(本文于2011年8月16日首发于果壳网死理性派主题站)
小时候我们都学过纸上谈兵这个词。其实历史上纸上谈兵的并非只有赵括一人,还有数学家。1914年一战期间,英国工程师弗雷德里克•兰彻斯特(我敢打赌这 家伙是一个死理性派)异想天开地用数学解析战争,创立了著名的兰彻斯特战斗模型。通过它,我们能很容易地发现以少胜多背后的数学故事,比如经典的萨尔浒之 战。
但在故事开始前,有必要说明的是,这只是 一个简化的数学模型 ,忽略了一些难以量化的因素,譬如天时、地利、人和以及政治因素,而它们对战争也有举足轻重的影响。事实上,从科学角度讲,研究结果仅对研究的模型有效。不过我们都知道,研究总是从基础模型开始的。
用兰彻斯特模型解析战争

这个著名的兰彻斯特战斗模型,实际上是一个讨论参战方战斗力和时间关系的模型,可以用来宏观地描述参战双方的战斗力损耗过程。这样说或许有些抽象,让我们 先思考一个问题,现在有两支军队 A 军和 B 军。A 军以精锐著称,但兵力只有 B 军的一半,B 军人多势众,但单兵作战能力平均只有A军士兵的一半, 除此之外它们其他方面全部是等同的。如果这两支军队交战,一支军队消灭另一支军队即为胜利,你认为谁将是这场战斗的赢家?读者们不妨先选定一个答案( A 胜、B 胜或者玉石俱焚),然后再来看看兰彻斯特战斗模型怎么说。
假设现在有一场战斗,交战的双方为甲方和乙方。我们规定它们在战斗中某一时刻的战斗力(冷兵器时 代,一般情况下就是部队中士兵的人数)分别是 x( t ) 和 y( t ) ,其中t表示时间。同时为方便起见,假设 x( t ) 和 y( t ) 都是关于 t 的连续可微函数,且恒为非负。换言之,双方的战斗力都是随着时间连续变化的,不可能在某一时刻发生突变(譬如《西游记》中的孙悟空从天宫搬来救兵),也不 可能在某一时刻有变化率的突变(譬如打架的时候被对方一巴掌打通任督二脉)。
在此基础上,我们再假设某方战斗力的变化都是由于敌方对它的攻击造成的,这样战斗力在某一时刻的变化量,便只和该时刻对方的战斗力正相关。
据此我们可以得出下面两个微分方程:
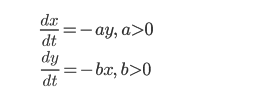
其中系数 a 和 b 分别是乙方和甲方对对方的杀伤率,也就是某方每单位战斗力能够对敌方造成的战斗力损耗。
这便是著名的兰彻斯特战斗方程。也许现在这个方程看上去还不够直观,但如果把它稍作变换,就可以得到这样的式子。

在上面的式子中,假设等式左右两边的值为正,当 x = 0 时,必有 y > 0 。这也就意味着当甲方的战斗力消耗殆尽的时候,乙军还有人活着,这种情况下自然是乙军获得了胜利。同理,当等式左右两边的值小于0时,甲军将取得胜利。那 当这个值等于0的时候呢?显然双方将惨烈地同归于尽,最终就像电影《赤壁》收尾处所说的那般:“大家都输了。”
更重要的是,上述这个式子还说明了 在战斗中双方的军事实力和各自军队战斗力的平方成正比 。这也就是著名的兰彻斯特平方律。
举个最简单的例子,倘若两支旗鼓相当的军队来火并的话,此时a = b , x0 = y0 = 1 ,这时候 a y₀ 2 = b x0 2 ,最终双方将同归于尽。但是倘若甲军去和一支人数是它的两倍,但每个士兵的实力只有他一半的乙军来打呢(这正是在前面提出的问题)?由 2a = b, y0 = 2x0 可得 a y0 2 / b x0 2 = 2。这表明占据人数优势的乙方将取得胜利,尽管他们的功夫都只有对手的一半。
更进一步来看后面这个例子,把 2a = b, y0 = 2x0 ,x = 0 这些条件都代入到上面给出的等式当中,可以得到y= √2 x。这意味着在乙军彻底消灭他的劲敌——精锐的甲军以后,自身兵力的损失还不到一半。如此事实无疑会让以精锐闻名的甲军感到压力山大,因为他们如果想要在 人数不变的情况下和乙军对敌而不败的话,至少要让自己的每个士兵的单兵作战能力达到乙军的四倍才行!
上面的例子让我们看到,兰彻斯特平方率直观地反映了对战双方的战斗力对比。金庸迷们一定记得《笑傲江湖》中东方不败独战令狐冲、任我行、向左使、任盈盈的 精彩片段,双方实际上打成平手。由此根据兰彻斯特平方率能推算出,东方不败的战斗力是其余四人战斗力平均值的16倍!也就是说,如果令狐冲、任我行、向左 使、任盈盈战斗力分别是100、80、60、40的话(平均战斗力70),东方不败的战斗力就是70 × 16 = 1120 。Ta的“天下第一”还真不是浪得虚名。
萨尔浒之战以少胜多的原因

从兰彻斯特到将近百年后的今天,历史开始显得久远。但这并不妨碍我们做一回“事后诸葛亮”,意行沙场,也来纸上谈兵,用激扬文字再指点当年战场。而这一回,我们就从数学角度来讲述那场经典的以少胜多——萨尔浒之战。
这是发生在万历四十七年(公元1619年),中国辽东的一场规模浩大且影响深远的大战。
在这场战役中,当时仅拥有约六万八旗子弟的后金军首领爱新觉罗•努尔哈赤,凭借着他老到的战略眼光,竟将兵力二倍于他、汹汹而来的大明王师打得惨败而归。 此战明廷丧师近五万,将官战死者亦有三百余人,其中还包括山海关总兵杜松这样的高级将领,可谓精锐尽失。若说当年李成梁对待努尔哈赤的态度是“为虺弗摧” 的话,经此一役的后金对明廷来说,已然是“为蛇若何”了。
然而在此战之前,并非人人都把后金当回事,至少此次战役中明军方面最高统帅、辽东经略杨镐大人就是如此。据说在萨尔浒战役之前,杨镐曾与努尔哈赤修书一 封,称大明王朝集结了四十七万大军将袭,并将出兵日期如实相告,似乎想以天朝神威威吓后金,好“不战而屈人之兵”。由此可见,在当时的杨镐看来,“消灭贼 酋”不过是手到擒来的事情,根本没有想到会有战败的可能。但是事实上,如果杨镐大人了解兰彻斯特模型,也许他就会发现,虽然他的兵力是对方的两倍,但他的 惨败却早在出师之日就已注定。
何出此言呢?不妨让我们用兰彻斯特战斗方程来分析萨尔浒之战。
当时努尔哈赤麾下的八旗子弟都是久经沙场的精锐,军队素质自然不可小觑。但明军亦有先进的武器和装备可与之抗衡,再加上常年和叛军作战的川军,以及由当年一代名将戚继光精心打造的浙军,军队的兵员能力也不在后金军之下。所以双方的杀伤率系数不妨看做是相等的。
那么兵力情况又是怎么样呢?我们在前面就已说过,后金军的兵力约六万人,而明朝方面的数据则是十二万。恰如前面的例子一般,后者的兵力是前者的两倍。换言 之,如果杨镐的大军就这么杀过来的话,似乎努尔哈赤唯一的方法,就是在对方到来之前,把自己手下兵士的作战能力提高到原来的四倍。
但是一个很有趣的事实是,在萨尔浒之战的交战过程中,始终占据兵力优势的却是后金。原来杨镐在进攻的时候竟把自己的军队分成了四路,而这四路军队不但没有 统一的调度,相互之间的通信也甚不灵便(实际战争中,有两路军队已经被努尔哈赤消灭了,第三路军竟还毫不知情)。这就使得本来兵力薄弱的努尔哈赤反倒拥有 了以众击寡、各个击破的局部战略优势。虽然后金的兵力只有明朝的一半,但是后金每次战斗中面对的兵力,却都只有自己的一半。
让我们来为这种战略局面算一笔帐。假设后金军和明军的杀伤率系数都是 1,战斗力以万人为单位,那么后金军的军事实力是:
![]()
假设明朝的四路军队中兵力平均分配,也就是每路有 3 万人(实际兵力部署与此相去不远),那么明朝的军事实力则是:
![]()
我们发现,拥有巨大人数优势的明军的军事实力和后金军其实是相当的!
当然,这里的计算有一个问题。我们给出的这种明军兵力分配方案,恰巧是使得它的军事实力总和最小,根据均值不等式可以知道,只要在实际分配的时候哪怕采用3.01,2.99,3,3这样的方案,明军不就能够打败后金了吗?
在这个模型下的确如此。但这要求当时的明军能如同岳飞所梦想的那样“文臣不爱钱,武臣不惜死”,军队在损失惨重的情况下依然坚持战斗到最后一人。那样的 话,努尔哈赤老兄真的是要操心下自己脑袋的去处了。可惜实际情况并非如此。古代战争的一个事实是,当某方的损失超过一定数量以后(这个数量通常还并不 高),往往会因为士气低落而溃散,在接下来就变成“追亡逐北”的场面了。这种情况下战斗变为屠杀,溃散军队的杀伤率约等于 0。所以战争的胜负绝大多数都不是因为一方把另一方完全歼灭,而是因为一方的士气已经无法维系。
所以不妨让我们假设双方都会在自身兵力损失达到一半的时候溃败。同时再把明军四路兵力的实际部署情况稍加调整,用 4,3,3,2 作为它的部署策略,此时的军事实力总值为38,高于后金军。第一场战斗后,后金的残余兵力 x1 满足如下方程:
![]()
解之得 x1 =2√6≈4.90 。也就是第一场战斗结束后后金军的剩余兵力约4.9万人。我们继续通过下面的方程求解 x2, x3, x4。
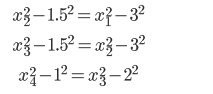
解之得
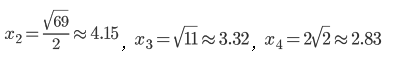
计算结果表明,四场战斗中每一场都是后金军的兵力占优,导致每一场战斗的胜者都是后金,所以最后的胜者也是后金——尽管总的军事实力明军更高。
要说明的是,这里对明军并没有任何的不公平。事实上这个模型还有些偏袒明军,因为在当时的历史条件下,明军士气的水平其实很难达到伤亡人数约一半时才溃 散。如果按照《窃明》中所说的标准——“除了处于死地外,最优秀的封建军队也不过能忍受一、两成的伤亡而不崩溃”来计算,当后金军取得胜利的时候,它所损 失的兵力也不过1.28万人,还远不到其初始兵力的三分之一。
借助数学工具,数百年后的我们可以轻松地计算出努尔哈赤必将取得大胜的结果 。可惜的是当时背负十数万将士性命的统帅杨镐并没有这样的觉悟,即使当开原总兵马林根据自身的经验向他提出“王师当出万全,宜并兵一路,鼓行而前,执取罪 人,倾其巢穴”这一清醒建议的时候,他也只是傲慢地坚持故我。如此无能的统帅最终葬送了大明的精锐之师。
结语

后来的事情是:万历四十七年二月二十五日,大明王师正式出征;三月初一,西路军遭努尔哈赤攻击,寡不敌众,全军覆没,总兵杜松战死;三月初三,北路军遭受 攻击,寡不敌众,全军覆没,总兵马林狼狈逃回;三月初五,东路军被后金军偷袭,猝不及防,全军覆没,总兵刘铤战死;三月初六,南路军接到三路大军战败的消 息后匆忙撤兵,后金军趁势追击,损伤惨重。结果正如我们这群事后诸葛亮所分析的一样,可惜我们的分析也正如开原总兵马林的意见一样,终无改这场战事的结 局。
也许在因这场惨败而下狱到他被处斩以前,杨镐也曾多次反思过这场过战斗。他或许无法像我们这样定量计算出战斗的结果,但至少也应该会对《孙子兵法》虚实篇里“以众击寡”这个词有一层新的理解吧。